概要
この記事では, 「効果検証入門」のポイントをまとめ, 書籍内で行われている分析を掲載していきます.
(本記事は自分が勉強したことのまとめ的要素が強いので, 手元に書籍がある状態でお読みいただくことをオススメします)
尚, 分析コードについては著者が提供しているGitHubからダウンロードもできますので, 実際に手を動かしてみたい方は参考にしてください.
今回は3章 傾向スコアについて取扱います.(P67~P90が該当)
傾向スコアは介入の割り当て確率が同じサンプル同士で比較をすればセレクションバイアスが軽減される, という考え方です.
まず前半では傾向スコアの基本的な考え方と効果推定の方法を, 後半では演習データを用いて実際に効果推定を行います.
また, 過去のブログについては以下をご参照ください.
3.1 傾向スコアのしくみ(P92~P96)
傾向スコアのアイデア
- 回帰分析では共変量の選択が難しく, 推定される効果もサンプルの特徴によって異なる場合とそうでない場合で異なってしまう
-
ここでは, 傾向スコア(Propensity Score)という介入の割当確率を用いて, 介入グループと非介入グループの中で性質の近いユーザ同士では介入がランダムに割当られている, という状況を作り出す
- 回帰分析では共変量の値(性別, 年代, 購買履歴等)が同じユーザの中ではランダムに割当られている(CIA)という仮定だったので傾向スコアでは条件が若干緩和されている
傾向スコアの推定
- 傾向スコアを用いるにはスコアを推定する必要があり, ここではロジスティック回帰を用いる. 以下がシグモイド関数である. \sigma(x) = \frac{1}{1+exp(-x)}
- これを用いることで介入変数Zを目的変数にしたときの回帰式が以下のようになり, 値が0~1におさまって介入があるかどうかの確率を算出できるようになる. (ただしβはパラメータ, uは誤差項)Z_i=\sigma(\beta X_i+u_i)
-
実際に第1章RCTで用いたデータを元に傾向スコアを求めてみる
- 介入の確率(treatmentが発生する確率)を「最後の購入からの経過月数」,「昨年の購入額」, 「昨年どのチャネルから購入したか」で推定している
# 傾向スコアの推定
## 使用するデータは第1章で作成済
ps_model <- glm(treatment ~ recency + history + channel,
data = biased_data,
family = binomial)
summary(ps_model)
3.2 傾向スコアを利用した効果の推定(P96~P111)
ここでは傾向スコアマッチングと逆確率重み付き推定(IPW)を紹介する
傾向スコアマッチング
-
傾向スコアマッチングは介入グループと非介入グループで先ほど算出した傾向スコアが近いサンプル同士をペアにしていき, ペア同士の目的変数の差を算出して平均をとる手法である
- ペアを作ることで傾向スコアが(ほぼ)同じもの同士であれば介入はランダムに決定されていると考えられ, セレクションバイアスの影響を受けない
- このようにして算出された期待値はATT(Average Treatment effect on Treated)と呼ばれる
- 次にRのMatchItパッケージを用いて分析を行う. 使用データは先ほどのロジスティック回帰と同じである
## 必要なライブラリを読み込む
library(tidyverse)
library(ggplot2)
library(broom)
library(MatchIt)
## 傾向スコアマッチング
m_near <- matchit(treatment ~ recency + history + channel,
data = biased_data,
### 最近傍マッチングを選択する
method = "nearest",
### 一度マッチしたサンプルを再度使うかどうか. FALSEだと二度とマッチングしない
replace = TRUE)
## 傾向スコアマッチング後のデータを抽出
match_data <- match.data(m_near)
## 処置効果の推定
PSM_result <- match_data %>%
lm(spend ~ treatment, data = .) %>%
tidy()
PSM_result
-
結果から, 約0.91ドル程度介入効果があるとわかる.
- 第1章でバイアスデータの介入グループと非介入グループを比較したときは0.98ドルと効果が過剰に推定されていたので, 若干改善されたと考えられる
逆確率重み付き推定(Inverse Probability Weighting : IPW)
-
IPWは傾向スコアをサンプルの重みとして利用し, 与えられたデータ全体での介入を受けた場合と受けなかった場合での期待値の差分をとる
- 実際のデータでは介入ありかなしかのどちらかしか観測できないが, 傾向スコアで欠損している部分を推定する
- 例えば傾向スコア=0.7のサンプルであれば70%がZ=1で30%がZ=0になるわけだが, このままでは傾向スコアが高いところにZ=1が集まり, 低いところにZ=0が集まってしまい, 結果的にバイアスがかかった期待値となってしまう
-
これの改善策として, 重み付き平均を用いる. イメージとしては傾向スコアの逆数を取り, サンプルの少ない部分の重みを増している
- 例えば傾向スコア=0.5であれば逆数をとると2になるので, サンプル数を2倍する
- 次にWeightItパッケージを用いてIPWの効果推定を行う
## パッケージの読み込み
library(WeightIt)
## IPW
weighting <- weightit(treatment ~ recency + history + channel,
data = biased_data,
### 傾向スコアを用いることを指定
method = "ps",
### ATEを推定する(ATTも指定可能)
estimated ="ATE")
IPW_result <- lm(spend ~ treatment, data = biased_data,
### weightsで利用する重みを指定
weights = weighting$weights) %>%
tidy()
IPW_result
- 結果は約0.87ドル程度売上を向上させる効果があるとわかる
より良い傾向スコアとは
- マッチング後共変量のバランスがとれているかに注目する
- cobaltパッケージのlove.plotを用いることで,標準化平均差の絶対値を表示できる
# 共変量バランスの確認
library(cobalt)
## 傾向スコアマッチング
love.plot(m_near, threshold = .1, abs = T)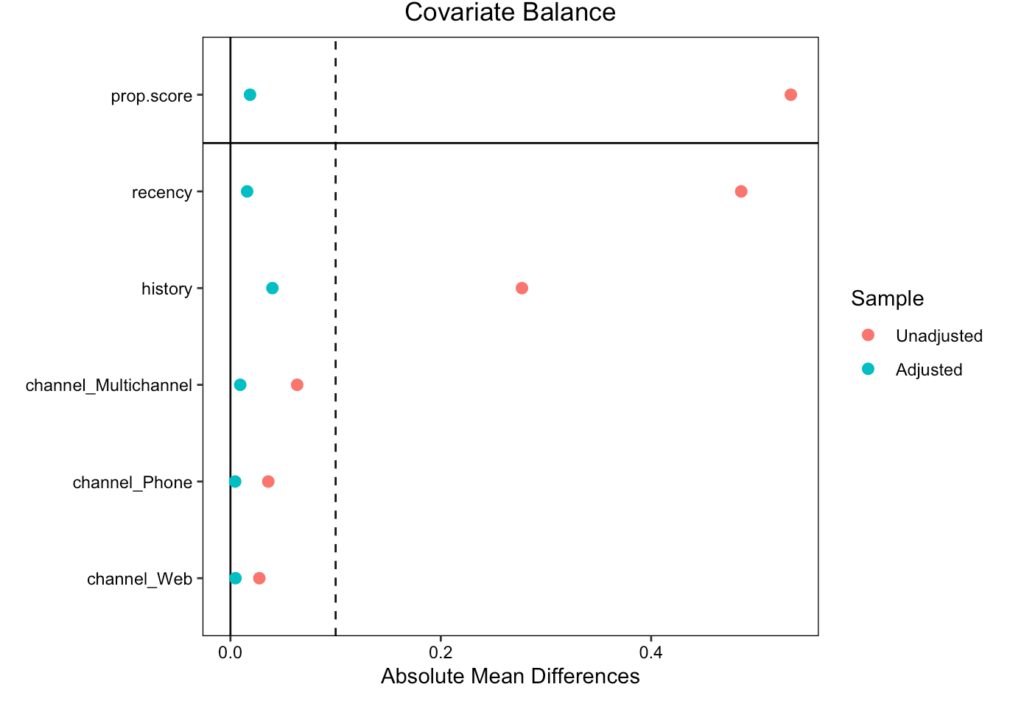
## IPW
love.plot(weighting, threshold = .1, abs = T)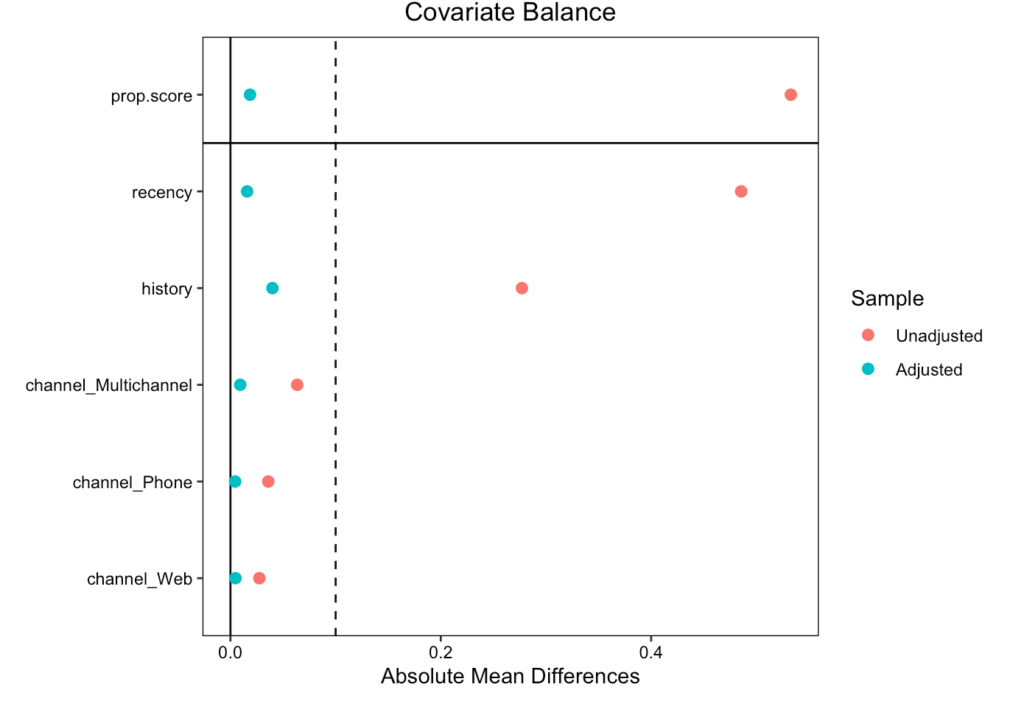
-
標準化平均差(ASAM)は平均の差を標準誤差で割ったものである
- これによって介入ありなしのグループ間で各変数の平均にどれくらい差があるのかが確認できる(もちろん差がないほうがいい)
- ASAMが0.1以下だと十分にバランスが取れていると考えられる
- バランスの改善の確認は様々あり, 本書では扱われていないが例えばQQプロットでも確認できる. 45度の直線上に並んでいるとバランスがよい(ただしlove.plotのほうが調整前後が表示されるので見やすい)
## QQプロットの表示
plot(m_near)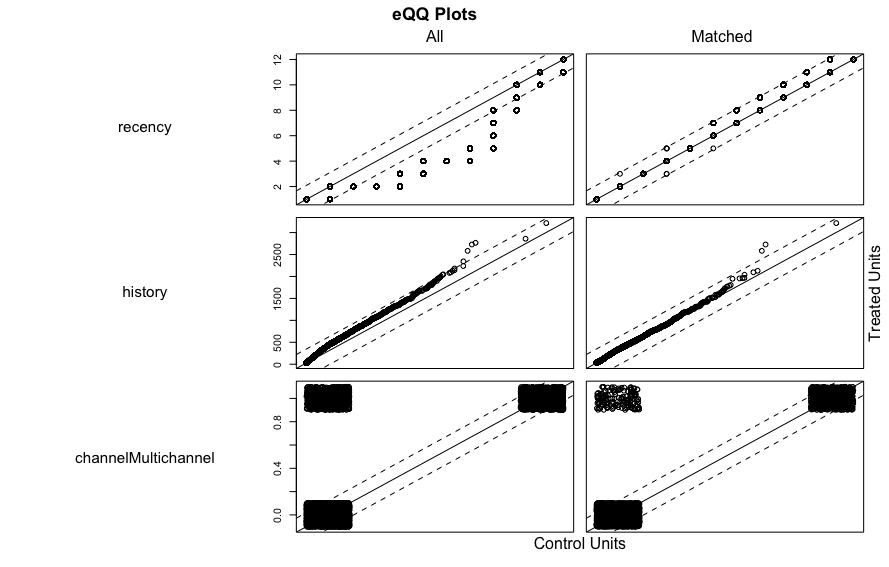
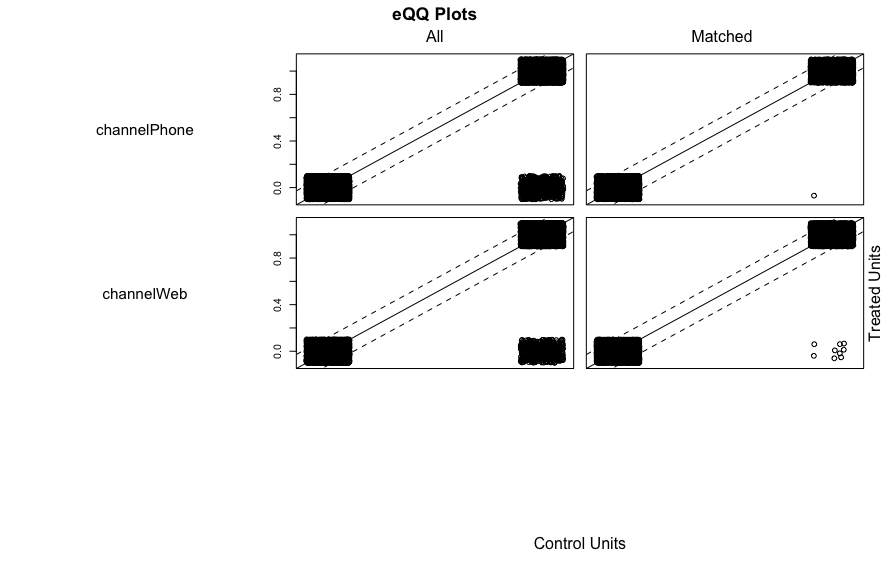
- 他にもcobaltパッケージの
bal.plotを使えば調整前後の傾向スコアの分布も確認できる
## 傾向スコアの分布の確認
bal.plot(weighting, var.name = "prop.score", which = "both",
type = "histogram", mirror = TRUE,
sample.names = c("Before", "After"))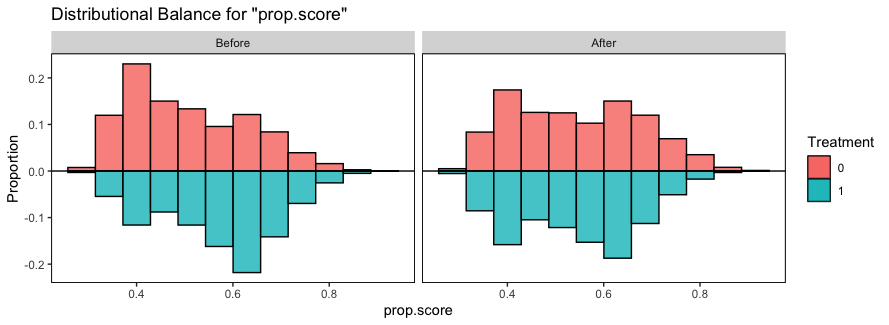
傾向スコアと回帰分析の比較
- 回帰分析は非常に手軽で簡単に取り組みやすいが, 共変量Xと目的変数Yの関係性を入念にモデリングする必要がある. ただし, モデルを正しく設定できれば標準誤差を小さくできるというメリットもある
- 傾向スコアは目的変数Yに対するモデリングをしなくて済むので, Yがどのようなしくみで決まるかに関してあまり情報がない場合便利であるが, 計算時間がかかるため大規模データの分析には向いていない
マッチングとIPWの差
-
基本的に両者の値は一致しない.
- マッチングでATTを推定する場合, Z=1となりそうな値を選び, そうでないものは捨てられる. そのためZ=1となりそうなもののみ残される. 結果, Z=1となりそうなサンプルの平均的な効果が求まる
- IPWでATEを推定する場合, 得られたすべてのデータにおける期待値を計算する. これはRCTを実行した場合の効果を推定することになる
- つまり, Z=1となるようなサンプルの効果が, すべてのデータにおける効果と同じでないと一致しない
3.3 機械学習を利用したメールマーケティング施策の効果推定(P111~P118)
- メールマーケティングのデータを用いてロジスティック回帰を実行し, メールが売上に与えた影響を推定する
データの作成
- メールデータをランダムに分割し, 訓練データとテストデータにする
-
訓練データの中からメールが配信されてないものだけ取り出し, 売上が発生する確率を予測するモデルを学習する
- これによって仮想的に傾向スコアを作り出せる
## ランダムに半分の行番号をサンプリング(元データ, サンプルする個数, 復元抽出するか)
train_flag <- sample(NROW(male_df), NROW(male_df)/2, replace = F)
## 訓練データ
### ランダムサンプリングしたものの中でメールを受け取ってない人を抜き出し
male_df_train <- male_df[train_flag, ] %>%
filter(treatment == 0)
## テストデータ
### train_flagでサンプリングされなかった残りの半分を抽出
male_df_test <- male_df[-train_flag, ]
## モデル作成
### conversion(メール配信後2週間後に売上が発生したか)を予測
predict_model <- glm(formula = conversion ~ recency + history_segment + channel + zip_code,
data = male_df_train,
family = binomial)- 次に, 作成したモデルをテストデータに当てはめ, 予測値を計算
-
次にpercent_rankでそれぞれの値が, 下から何%にあたるかでランク付する
- 値が0.8であれば下から80%であり, 80%の確率でメールが配信される
-
最後にランダムにメール配信するかどうかを割り振るために二項分布に従った乱数を先ほどのパーセントランクを用いて発生させる. そして, 実際にメールが配信されたものだけ残す
- よって, 配信確率が高いサンプルほどメール配信ダミーが割り当てられる可能性が高くなる
## メールが配信される予測値を計算
pred_cv <- predict(predict_model, newdata = male_df_test, type = "response")
## サンプル内でパーセントランクを計算
pred_cv_rank <- percent_rank(pred_cv)
## 二項分布に従う乱数を発生
### nで発生させる乱数の数を指定, sizeは試行回数
mail_assign <- map(pred_cv_rank, rbinom, n = 1, size = 1)
## 配信ログを作成
ml_male_df <- male_df_test %>%
### 仮想のメール配信履歴, パーセントランクを追加
mutate(mail_assign = mail_assign,
ps = pred_cv_rank) %>%
### 実際にメール配信をされた人と実際にメール配信されなかった人だけ残す
filter((treatment == 1 & mail_assign == 1) |
(treatment == 0 & mail_assign == 0))RCTと平均の比較
- まずはテストデータがランダムにメール配信をした場合の結果を確認する
rct_male_lm <- lm(spend ~ treatment, data = male_df_test) %>%
tidy()
rct_male_lm
- 続いて, 先ほど作ったデータで計算してみる
ml_male_lm <- lm(spend ~ treatment, data = ml_male_df) %>%
tidy()
ml_male_lm
-
効果がRCTの時に比べて過剰推定されていることがわかる
- これは元々売上が発生しそうなユーザに偏ってメール配信がされるようなデータとなっているからである
傾向スコアを用いた分析
-
傾向スコアを用いた場合で先ほどパーセントランクで介入を割り当てたデータを使う
- Matchingパッケージの
Match関数を用いる
- Matchingパッケージの
library(Matching)
## Yは目的変数, Trは介入変数, Xは傾向スコアのデータ
PSM_result <- Match(Y = ml_male_df$spend, Tr = ml_male_df$treatment,
X = ml_male_df$ps, estimand = "ATT")
summary(PSM_result)
- p値から効果があるとは言い切れない
-
次にIPWで推定する
- 重み付き最小二乗法を行うことで, 求めた傾向スコアによる重みつき平均を反映させている
## IPWの推定
### ATEを推定
### psで傾向スコアを指定
W.out <- weightit(treatment ~ recency + history_segment +
channel + zip_code,
data = ml_male_df,
ps = ml_male_df$ps,
method = "ps",
estimand = "ATE")
## 重み付けしたデータでの共変量のバランスを確認
love.plot(W.out, threshold = .1, abs = T)
## 重みづけしたデータでの効果の分析
### weightsで重みを指定している
IPW_result <- ml_male_df %>%
lm(data = .,
spend ~ treatment,
weights = W.out$weights) %>%
tidy()
IPW_result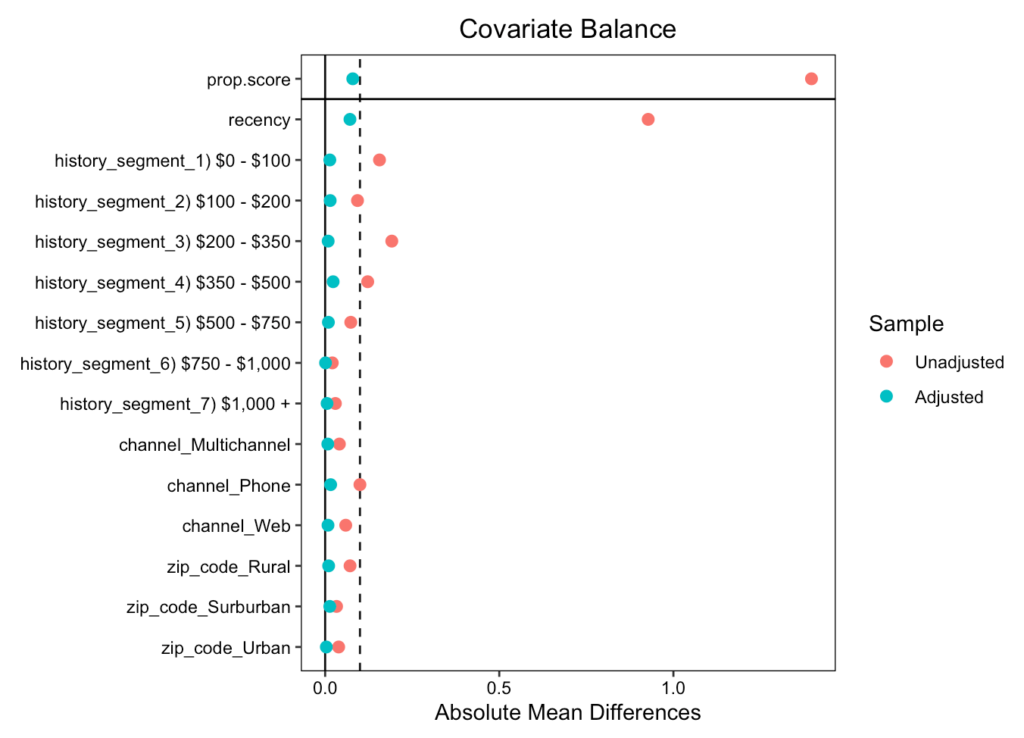

-
統計的に有意な結果となり, かつRCTの時の結果にも近づいている
- ただし, 結果が若干不安定であり発生させる乱数の影響を受けやすくなっている(場合によってはRCTの結果と大きく異なる場合もある)
- 今回はメールの配信が購買予測に基づいてある程度ランダムに行われていたが, 一定値を超えたら配信するなどのランダム性のない設定がされている場合はこの手法が使えず, 5章で取り扱う回帰不連続デザイン(RDD)を利用する
Lalondeデータセットの分析(P118~P131)
導入
-
Lalondeデータセットを用いた分析を行う
- 失業者に対してランダムに短期的な就労経験を与えることを介入とし, 所得に影響があるのかを測定する
- ここで, データにバイアスを発生させるため, NSW内の非介入グループを削除し代わりにCPSという別の調査データを非介入グループとした(CPS3はある時点で雇用をされていないサンプル, つまりNSWに割と近い傾向を持つデータ)
- このデータからいかにバイアスを取り除いて本来の実験結果に近づけるかが主題となる
## STATAやSASなどのデータを読み込むパッケージ
library(haven)
## データの読み込み
cps1_data <- read_dta("https://users.nber.org/~rdehejia/data/cps_controls.dta")
cps3_data <- read_dta("https://users.nber.org/~rdehejia/data/cps_controls3.dta")
nswdw_data <- read_dta("https://users.nber.org/~rdehejia/data/nsw_dw.dta")
## cps1を非介入グループとして取り込む
cps1_nsw_data <- nswdw_data %>%
filter(treat == 1) %>%
bind_rows(cps1_data)
## cps3を非介入グループとして取り込む
cps3_nsw_data <- nswdw_data %>%
filter(treat == 1) %>%
bind_rows(cps3_data)RCTによる結果の確認
- NSWの実験データ内のみで職業訓練の収入に対する効果を推定する. よって結果はRCTが実現できているものと考えられる. ここでは以下のモデル式を想定する
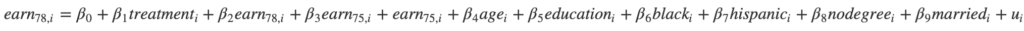
## 共変量付きの回帰分析
nsw_cov <- lm(formula = re78 ~ treat + re74 + re75 + age + education + black + hispanic +
nodegree + married,
data = nswdw_data) %>%
tidy() %>%
### 介入効果のみ抽出
filter(term == "treat")
nsw_cov
- RCTデータでは介入により1676ドル程度の収入アップが見込まれる
回帰分析による効果の推定
- まず先ほど作成したバイアスのあるデータで回帰分析を実行してみる
cps1_reg <- lm(formula = re78 ~ treat + re74 + re75 + age + education + black + hispanic +
nodegree + married, data = cps1_nsw_data) %>%
tidy() %>%
filter(term == "treat")
cps1_reg
cps3_reg <- lm(formula = re78 ~ treat + re74 + re75 + age + education + black + hispanic +
nodegree + married, data = cps3_nsw_data) %>%
tidy() %>%
filter(term == "treat")
cps3_reg
- cps1_regでは結果が過少推定されており, かつ統計的にも有意ではない
- 理由としてはNSWのサンプルはCPSのサンプルより平均的に年齢や収入が低く, 結果として平均的な効果が低くなってしまう
- cps3_regでは比較的RCTに近い結果が出ているが, これは調査時に雇用されていないサンプルに限定しているため
- ただしこれはその状況ごとに対応する必要があり, ルールの妥当性について都度検討することが求められる
傾向スコアによる効果の推定
- 傾向スコアマッチングにより, NSWのデータの傾向に近い状態を作り出す
## 最近傍マッチング
m_near <- matchit(formula = treat ~ age + education + black + hispanic +
nodegree + married + re74 + re75 + poly(re74^2) + poly(re75^2),
data = cps1_nsw_data,
method = "nearest")
## 共変量バランスの確認
love.plot(m_near, threshold = 0.1, abs = T))
## マッチングしたデータの作成
matched_data <- match.data(m_near)
## マッチング後のデータで効果推定
PSM_result_cps1 <- lm(re78 ~ treat, data = matched_data) %>%
tidy()
PSM_result_cps1
- 1877ドルと推定され, 先ほどよりRCTの結果に近づいた
- 共変量のバランスもとれている
-
次にIPWで推定を行う
- 今回, サンプルコードにあるweightsの指定では計算がうまくいかなったため, こちらのサイトを参考にIPWによる重みを計算し, 効果を推定した
# IPWの推定
## 回帰式の設定
ps_formula <- treat ~ age + education + black + hispanic + nodegree + married + re74 + re75 + I(re74^2) + I(re75^2)
## ロジスティック回帰
fit_logistic <- glm(ps_formula, data = cps1_nsw_data,
family = binomial(link = "logit"))
## 傾向スコアの抜き出し
### それぞれのサンプルの予測値をデータに追加する
cps1_nsw_data$ps_logit <- fitted(fit_logistic)
## 傾向スコアを利用して重みを推定する
cps1_nsw_data <- cps1_nsw_data %>%
mutate(w_ate = ifelse(treat == 1,
1 / ps_logit,
1 / (1 - ps_logit)))
## 共変量のバランスを確認
weighting <- weightit(ps_formula, data = cps1_nsw_data,
method = "ps", estimand = "ATE")
love.plot(weighting, threshold = 0.1, abs = TRUE, grid = TRUE)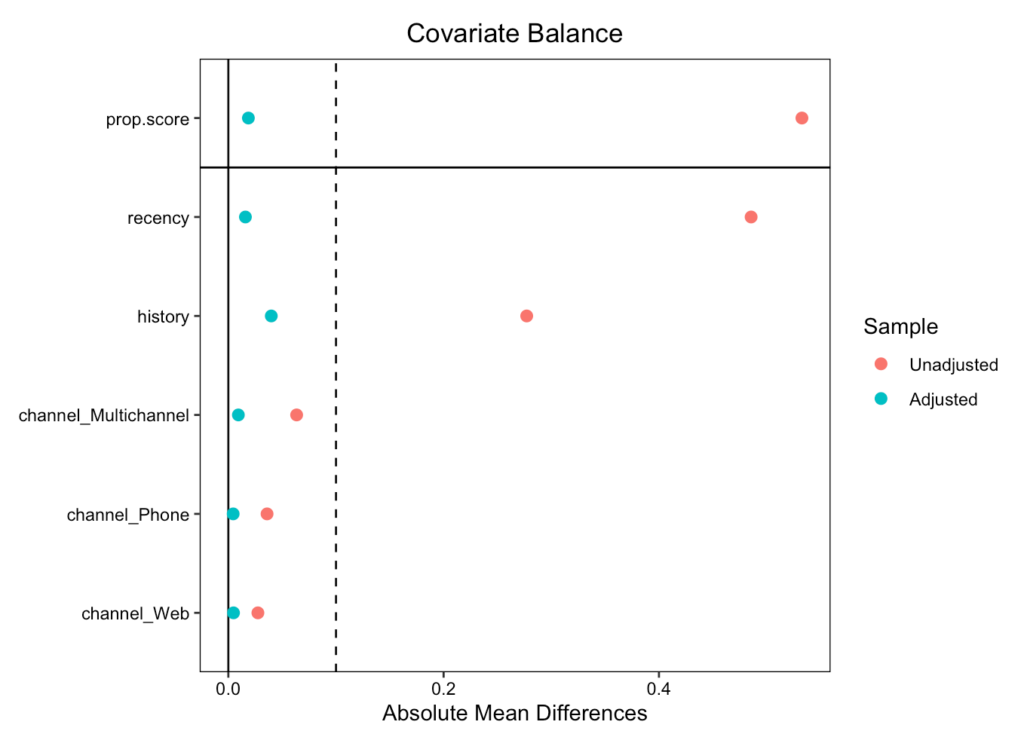
## 重み付きデータでの効果の推定
IPW_result <- lm(data = cps1_nsw_data,
formula = re78 ~ treat,
weights = w_ate) %>%
tidy()
IPW_result
- 共変量のバランスもあまり調整できておらず, 推定結果は大きくマイナスとなっている
-
IPWの場合, 介入グループと非介入グループで大きく傾向が異なる場合, 分析結果が不安定なことがある
- これはIPWが傾向スコアが小さいサンプルの重みが大きくなってしまうからであり, CPSにのみ含まれるサンプルの重みが大きな値をとってしまう(CPSはサンプル数も多く, データのばらつきも大きい)
- CPSは職業訓練が必要なく, 収入も安定しているサンプルが多いため, 結果非介入グループの期待値が大きくなってしまう
おわりに
本章では傾向スコアを用いた分析手法を学びました. 分析を行うにあたり, 自分がどんな仮定を置いているのかや, どんな効果を推定したいのかをしっかりと設定することで, 信頼できる結果かどうかが判断できます. 例えば調査していない共変量のバイアスは測定できません. 従ってドメイン知識や事前背景を押さえておくことも重要です.
次回, 第4章では介入前後のデータを用いる差分の差分法(DID)を扱っていきます.
最後までお読みいただきありがとうございました.