計算をスクラッチで実装することの意味
RやPythonでは単回帰分析を数行で書けます。
試しにRで書いてみます。
[code language="R"] n = 10 # データ数 x = c(30, 10, 50, 80, 50, 55, 65, 70, 85, 85) y = c(30, 40, 40, 35, 55, 50, 75, 80, 90, 95) result = lm(y~x) # 回帰 summary(result) # 結果 [/code]
出力結果はこちら
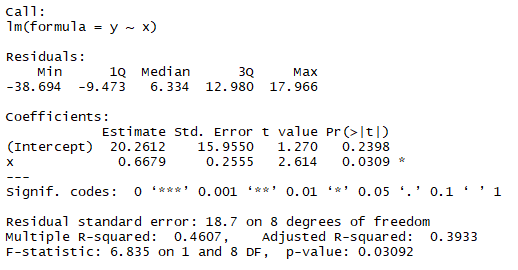
とても簡単にできます!
lm()を使うために、lm()の中身でどんなことが行われているか知っている必要はありません。
単回帰分析のようなメジャーな分析手法は、Rでは標準関数として実装されていたり、Pythonではsklearnというライブラリで実装されていたりするので簡単に利用することが出来ます。
しかし少しニッチな分析手法を試そうとしたときに、欲しいライブラリがRにはあるのにPythonにない、PythonにはあるのにRにはない、といった機会に遭遇します。
また、そんなライブラリは存在しない、なんてこともあります。
そういったときに、定義に従って数式の理解を進め、プログラミングによって再現していくことが必要になることがあります。
今回は簡単な例として、単回帰分析の定義に従って最低限の言語の機能だけを用いて、上記の結果を再現してみたいと思います。
単回帰分析とは
2変数xとyがあり、 x によって y が決定されるという関係を、以下のように表現してみます。
y=f\left( x\right)ここで y=f\left( x\right) は任意の関数です。
2変数xとy の一方を用いて、もう一方の変数を求めるために、この任意の関数をモデリングすることを単回帰分析といいます。
以下のような2次元データ、(x_1,y_1),(x_2,y_2),..,(x_i,y_i),..,(x_{10},y_{10})を考えます。
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x_i | 30 | 10 | 50 | 80 | 50 | 55 | 65 | 70 | 85 | 85 |
| y_i | 30 | 40 | 40 | 35 | 55 | 50 | 75 | 80 | 90 | 95 |

yをxの一次関数で予測する以下のようなモデルを考え、この 切片αと傾きβを計算によって求めます。
y=\alpha+\beta x誤差項
2次元データ、(x_1,y_1),(x_2,y_2),..,(x_i,y_i),..,(x_{10},y_{10}) があるとき、yをxの一次関数で予測するモデルを考えます。
y=\alpha+\beta x_i+\varepsilon_i\alpha+\beta x_iはxの一次関数で、 \varepsilon_i はそれ以外の誤差項を表します。

最小二乗法による切片αと傾きβの計算
y=\alpha+\beta x_i+\varepsilon_iを変形して、
\varepsilon_i=y-(\alpha+\beta x_i)誤差の二乗和を最小にするようなαとβを求めます。
\min \sum ^{n}_{i=1}\varepsilon ^{2}_{i}=\min \sum ^{n}_{i=1}\left[ y_{i}-\left( \alpha +\beta x_{i}\right) \right] ^{2}これを αとβそれぞれで微分して0と置いて解いていくと、 (ここは数式を書くのが面倒になったので省きます)
\overline {y}= \dfrac {\sum ^{n}_{i=1}y_{i}}{n}
\overline {x}= \dfrac {\sum ^{n}_{i=1}x_{i}}{n}
と置いて、
\beta =\dfrac {\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) }{\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right) ^{2}}
\alpha = \overline {y} - \beta \overline {x}
となります。
すなわちこの計算は、xとyの共分散と、xの分散を求めることで簡単に解けることがわかりました。
以下では上記で導いた結果を用いてRを使って実装を行ってみたいと思います。
Rによる実装
データの生成
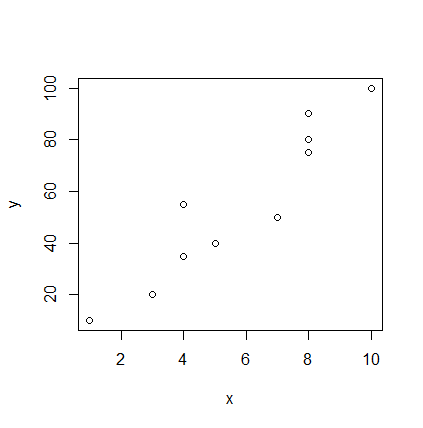
[code language="R"] n = 10 x = c(30, 10, 50, 80, 50, 55, 65, 70, 85, 85) y = c(30, 40, 40, 35, 55, 50, 75, 80, 90, 95) plot(x, y, xlim = c(0,100), ylim = c(0,100)) # xとyのプロット [/code]
x、yの平均
[code language="R"] x_mean = sum(x) / n y_mean = sum(y) / n print(x_mean);print(y_mean)
[1] 58
[1] 59
[/code]
x、yの偏差
[code language="R"] x_sdv = array(x - x_mean) y_sdv = array(y - y_mean) print(x_sdv);print(y_sdv)
[1] -28 -48 -8 22 -8 -3 7 12 27 27
[1] -29 -19 -19 -24 -4 -9 16 21 31 36
[/code]
x、yの分散
[code language="R"] x_var = as.numeric(x_sdv %% x_sdv / n) y_var = as.numeric(y_sdv %% y_sdv / n) print(x_var);print(y_var)
[1] 536
[1] 519
[/code]
xとyの共分散
[code language="R"] xy_cov = x_sdv %*% y_sdv / n print(array(xy_cov))
[1] 358
[/code]
α、βの計算
[code language="R"]
betaの計算
beta = as.numeric(xy_cov / x_var)
alphaの計算
alpha = y_mean - beta * x_mean
結果の確認
print(c(alpha, beta))
[1] 20.2611940 0.6679104
[/code]
lm()とスクラッチの結果比較
これでαとβを計算することが出来ました!lm(y~x)の結果と比較してみましょう。
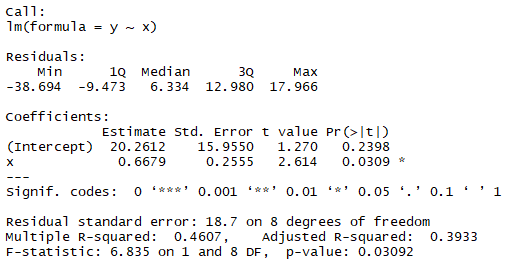
Interceptが20.2612、xが0.6679とありますね。 どうやらうまくいってそう。
今回は以上になります。ありがとうございました。