目的
- VAEの構造を理解する
- VAEの学習方法を理解する。(次回)
前提知識
- 基本的なニューラルネットワークの知識
- 確率・統計の基本的な知識(条件付き確率分布、ベイズの定理等)
VAEの目的
VAEは様々な分野で活用されていますが、画像分野では特に画像生成のモデルとして利用されています。詳しくは前回のブログをご確認ください。
特に画像生成の文脈でVAEを使用する目的は、持っている画像データセットX=\{x_1,\cdots,x_N\}を使って、データセットX内に「ありそうな」画像を生成することになります。「ある」データでは意味がありません。なぜなら、実際にあるデータを生成してもそれは単なるデータの複製になってしまうからです。あくまで、目的は「ありそうな」データの生成することという点を認識しておいてください。(後程触れますが、学習時には「ある」データの復元を行うことで学習しています。)
VAEの構造
以降では、VAEがどんなモデルなのかをより細かく確認していきます。

デコーダーp(x|z)
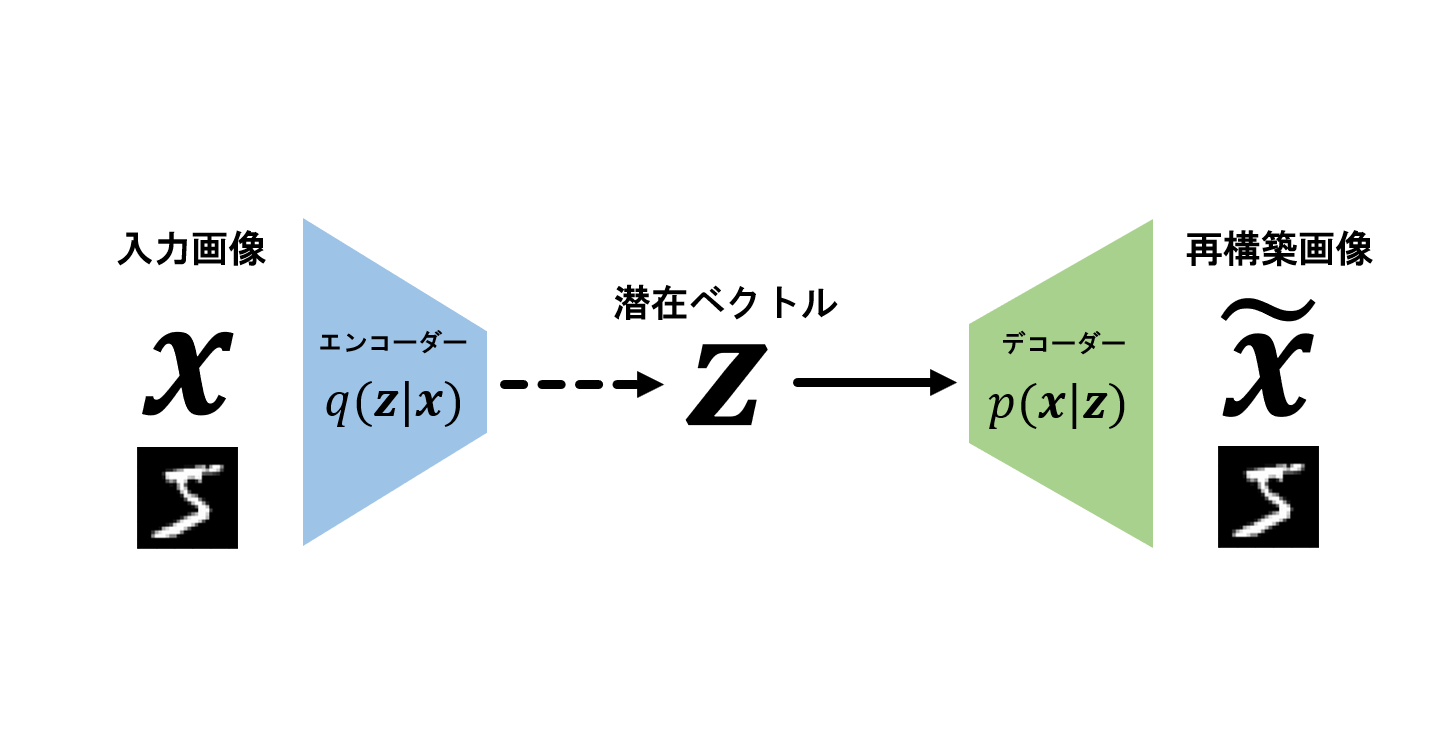
上画像が、VAEのアーキテクチャになります。まず、潜在ベクトルから右側の部分について説明します。
なんらかのベクトルz (上では潜在ベクトルと呼んでいます)を入力して、画像xを生成するモデルp(x|z)を考えます。
具体的には、以下のようなモデルです。
ここで、f(z;\theta)は\thetaをパラメータ(重みなど)とするニューラルネットワーク(以降NN)であるとします。NNを用いているのは、画像が非常に複雑な構造を持っているため、画像を生成するために表現力の高い関数が必要となるためです。ちなみにこのモデルをデコーダーと呼びます。
このモデルは、f(z;\theta)、すなわちNNの出力を平均とし、画像xを確率変数とする正規分布となります。(正規分布でない場合もありますが、今回は簡単のために正規分布とします)
ここでなんらかのベクトルとしていたzにも確率分布を導入し、
p(z)=\mathcal{N}(0,I)
とします。
すると、p(z)とp(x|z)を用いて以下のような流れで画像を生成することができるようになります。
- p(z)からz^{\ast}をサンプリング
- p(x|z^{\ast})からx^{\ast}をサンプリング
これで画像を生成することができるようになりました。しかし、まだ一切学習をしていないので、デコーダーの中のNN f(z;\theta)のパラメータ\thetaを学習していく必要があります。(次の節)
デコーダー
デコーダーq(z|x)は、画像xを入力とする潜在ベクトルzを確率変数とする確率分布です。詳しくは後程説明したいと思います。
VAEの学習
学習に際しては、パラメータの良さを表す関数を設定する必要があります。以降では、目的関数の設計について確認していきます。
これまでに導入して確率分布はp(z)とp(x|z)の二つです。これらの確率分布を用いるとベイズの定理から、以下の数式が成り立ちます。
p(z|x)=\frac{p(x|z)p(z)}{p(x)}右辺の分母に現れるp(x)はデータxの生成確率を表しています。ということはp(x)が大きい=設計したモデルp(x|z)p(z)がもっともらしいということが言えそうです。ちなみに
p(x)=\int p(x|z)p(z) dz=\int \mathcal{N}(x|f(z;\theta),\Sigma_p)\mathcal{N}(z|0,I)dzですが、これは一般に解析的な計算ができません。これは、\mathcal{N}(x|f(z;\theta),\Sigma_p)の中にNNが含まれている点に由来しています。
そこで、一般にエビデンス\log p(x)の下界(ELBO)を目的関数とし、最大化する方法がとられます。(\log xは単調増加関数なので、p(x)の最大化と\log p(x)の最大化は等価な問題です。)目的関数の設計に用いるp(z|x)を近似する分布をq(z|x)=\mathcal{N}(z|g(x;\phi),\Sigma_q)としておきます。(q(z|x)の解釈は後程)これを用いると、以下のよう\log p(x)に対する下界を導出することができます。
\begin{aligned}\log p(x)&=\log \int p(x,z)dz\\&=\log \int q(z|x)\frac{p(x,z)}{q(z|x)}dz\\&\geq\int q(z|x)\log \frac{p(x,z)}{q(z|x)}dz\\&=\mathbb{E}_{q(z|x)}[\log p(x|z)]-KL[q(z|x)||p(z)]\\&=\mathcal{L}(\theta,\phi)\end{aligned}第二式から第三式への変形にはイェンセンの不等式を用いています。この下界をELBO(Evidence Lower BOund)、あるいはエビデンス下界と呼びます。この下界は変分ベイズ法で一般的に用いられる目的関数です。
この値をデコーダーp(x|z)のパラメータ\thetaとエンコーダーq(z|x)のパラメータ\phiについて最大化することで、p(x)の最大化が近似的に達成されます。
すなわち、適切なp(x|z)を学習することができるのです。
ここで、気になる点が2点ほどあります。
-
なぜq(z|x)なるものを導入したのか?
⇒ 次節で説明します -
ELBO\mathcal{L}(\theta,\phi)は\theta,\phi について最適化できるの?(勾配計算できるの?)
⇒ 特定のケースで勾配計算が可能です。(勾配法による最適化が可能です)
2.の詳細については、このブログの後編で解説したいと思います。
モデルの概要についてのみ気になる方は、前編であるこのブログで十分かと思います。
デコーダーq(z|x)の解釈

なぜq(z|x)なるものを導入したのかについてですが、理由は「デコーダーのパラメータ\phiの学習に必要だったから」であると言えます。要するに、損失関数ELBOを設計し、最適化するうえで必要になる補助的な確率分布がq(z|x)というわけです。
これを導入すると、先ほど紹介したELBOの正体が見えてきます。
\mathcal{L}(\theta,\phi)=\mathbb{E}_{q(z|x)}[\log p(x|z)]-KL[q(z|x)||p(z)]
第1項の期待値の中は、ある潜在ベクトルzに対して、画像xが生成される尤度であると解釈できます。そして、それをq(z|x)について期待値計算しています。要するに、エンコーダーq(z|x)からのサンプルzに対して、どの程度うまく画像xを再現できそうかを計っているのが第1項と言えます。
一方で第2項はエンコーダーq(z|x)がp(z)=\mathcal{N}(0,I)とどの程度近いかを表しています。これを小さくすることは、デコーダーq(z|x)をp(z)に近づけることに対応しています。最初に触れたように、初期の生成過程ではp(z)からのサンプルを入力として、p(x|z)による画像の生成を行っていました。なので、エンコーダーq(z|x)がp(z)と全く違うと、デコーダーの入力として不適切になってしまいうので、こういったある種の正則化項を必要としています。
まとめると、エンコーダーq(z|x)は画像から「可能な限り画像xの情報を保持した」潜在ベクトルzを獲得するように学習され、デコーダーp(x|z)はエンコーダーから与えられたベクトルzを用いて元画像xを可能な限り再現できるように学習していきます。
第二項によりq(z|x)とp(z)は近い確率分布です。なのでp(z)からの適当なサンプルに対して「ありそうな」画像を生成できようになります。
VAEの用途
生成モデルの例としてVAEを紹介してきました。実際に上で学習したデコーダーp(x|z)は生成器として利用できます。一方でq(z|x)は画像をベクトルに変換する手法としてfew-shot学習などで用いられるようです。
まとめ
今回はVAEの目的、アーキテクチャに加えて学習方法を簡単に説明しました。次回のブログでは、今回紹介した目的関数を用いてどのように学習していくかについて解説していきます。
参考文献
Kingma, D. P., & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
須山敦志(2019) :『ベイズ深層学習』, 講談社

